A truly lazy OrderBy in LINQ
Jon Skeet recently discussed what it means to be “lazy” (in the context of LINQ to Objects). He introduced some new definitions based on how the operator processes the source sequence. Another aspect (which Jon didn’t cover) is how lazily the operator produces output when its results are enumerated.
Let’s take a concrete example: what’s the difference in running time between these two statements?
var count1 = bigCollection.Count();
var count2 = bigCollection.Take(10).Count();
Assuming “bigCollection” doesn’t implement ICollection
var count1 = bigCollection.OrderBy(x => x).Count();
var count2 = bigCollection.OrderBy(x => x).Take(10).Count();
The running time of both these statements is actually about the same. Even though the OrderBy documentation states that “This method is implemented by using deferred execution. … The query represented by this method is not executed until the object is enumerated”, what that actually means is that the sort isn’t performed until the first call to MoveNext on the enumerator returned by OrderBy. But when that first call to MoveNext happens, the entire input is sorted, even though only the smallest ten items are required.
There’s no reason this needs to be the case; Wikipedia has an extensive discussion on efficiently selecting the k smallest elements from a collection. Quicksort is a natural choice for implementing such an algorithm: since it divides the array in half around a pivot element, it’s easy to defer sorting the right-hand side (i.e., elements greater than the pivot) until we know that the consumer needs them.
Using the yield statement will make implementing a lazy algorithm easy, but
quicksort is typically implemented recursively, which is hard to combine with
yield (without using foreach statements that simply yield the recursive
output). Instead, we can use a stack to maintain the state of the recursion
and implement it in an iterative fashion. As we divide the array in half, we
push the pieces that are not yet sorted onto a stack. When we detect that a
section of the array is completely sorted, we yield those elements to the
caller. This ensures that the sorting work is not done until it’s needed.
In practice, this implementation performs very well; the following graph shows
how long it takes to call .OrderBy(x => x).Take(100) on arrays (of integers)
of various sizes. The blue line shows the performance of the standard .NET
implementation, while the red line shows how the new lazy implementation out-
performs it.
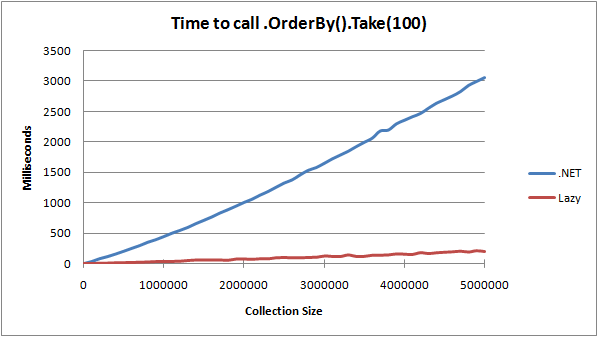
Not only that, but the algorithm is no slower if you end up enumerating the
entire sequence (and thus sorting every element). The full source code is
available at GitHub
(specifically in the OrderedEnumerable.cs
and ElementComparer.cs files);
the following excerpt illustrates the core
concepts. (Note that this simplified version doesn’t maintain compatibility
with OrderBy: specifically, the sort is not stable, and you can’t chain a
.ThenBy to the resulting sequence. The full implementation at GitHub does
not have these limitations.)
/// <summary>
/// Sorts the elements of a sequence in ascending order according to a key.
/// </summary>
/// <param name="source">A sequence of values to order.</param>
/// <param name="keySelector">A function to extract a key from an element.</param>
/// <param name="comparer">An <see cref="IComparer{T}"/> to compare keys.</param>
/// <returns>An <see cref="IEnumerable{TSource}"/> whose elements are sorted according to a key.</returns>
/// <remarks>This method only sorts as much of <paramref name="source"/> as is
/// necessary to yield the elements that are requested from the return value. It performs an
/// unstable sort, and can't be chained to Enumerable.ThenBy.</remarks>
public static IEnumerable<TSource> LazyOrderBy<TSource, TKey>(this IEnumerable<TSource> source,
Func<TSource, TKey> keySelector, IComparer<TKey> comparer)
{
// convert the entire input to an array, so we can sort it in place
TSource[] array = source.ToArray();
// track index of the last (sorted) item that was output
int index = 0;
// use a stack to turn a recursive algorithm into an iterative one
Stack<Range> stack = new Stack<Range>();
// start by processing the entire array
stack.Push(new Range(0, array.Length - 1));
while (stack.Count > 0)
{
// get current range to sort
Range currentRange = stack.Pop();
if (currentRange.Last - currentRange.First == 0)
{
// base case: we only have one item; it must be sorted
yield return array[index];
index++;
}
else
{
// recursive case: partition the array into two halves and "recurse" on each half
int pivotIndex = Partition(array, currentRange.First, currentRange.Last, keySelector, comparer);
// pushing the second half of the range first means that it will be sorted last
stack.Push(new Range(pivotIndex + 1, currentRange.Last));
stack.Push(new Range(currentRange.First, pivotIndex));
}
}
}
// Partitions an array into two halves around a pivot, returning the index of the pivot element.
// This algorithm is taken from Introduction to Algorithms (MIT Press), p154.
private static int Partition<TSource, TKey>(TSource[] source, int first, int last, Func<TSource, TKey> keySelector,
IComparer<TKey> comparer)
{
// naively select the first item as the pivot
TKey pivot = keySelector(source[first]);
// walk the array, moving items into the correct position
int left = first - 1;
int right = last + 1;
while (true)
{
do
{
right--;
} while (comparer.Compare(keySelector(source[right]), pivot) > 0);
do
{
left++;
} while (comparer.Compare(keySelector(source[left]), pivot) < 0);
if (left < right)
{
TSource temp = source[left];
source[left] = source[right];
source[right] = temp;
}
else
{
return right;
}
}
}
// Range represents an inclusive range of indexes into the array being sorted.
private struct Range
{
public Range(int first, int last)
{
m_first = first;
m_last = last;
}
public int First { get { return m_first; } }
public int Last { get { return m_last; } }
readonly int m_first;
readonly int m_last;
}
Posted by Bradley Grainger on April 08, 2010